- 2022/07/11 18:40
面積迷路
先日(と言っても随分前)
本屋さんのパズルコーナーでウロウロしていると、気になる本を発見。
本の名前は「新 面積迷路」
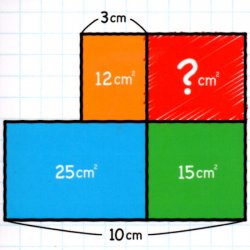
表紙には、このような問題が。
どうやら…
周囲にある四角形の
辺の長さや面積を元に「?」を導きだす。
そんなパズルのようです。
一目見て…
私(心の声)「面白そう」
+゚*。:゚+(人*´∀`)+゚:。*゚+.
はい、即買いです(苦笑
普通に考えれば…
面積=縦の長さ×横の長さ
なので、
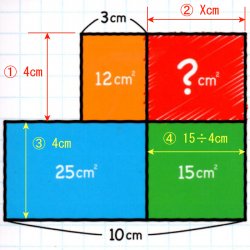
右図でいう(1)(2)を出せば(?)が出る。と。
(1) 12÷3=4
(2)を導く前段階として
水色の面積25と緑色の面積を足して40。
(3) 40÷10=4
あぁ、じゃあ(4)は 15÷4=3.75 だよね。
と、なる。
んが。 このパズルの醍醐味というのが…
「小学生の算数だけで解ける」という部分。
もっと平たく言えば、分数・少数は使わない。ココ。 Σ(`ロ´ノ)ノ
もちろん面積計算なので強引に分数・少数を使ったり、
問題によっては連立方程式でイケたりするけど…
解法を見ると…
「あぁ… il||li _| ̄|○ il||li」と、納得させられると共に
妙にややこしく考えている自分に軽い嫌悪感すら覚えます(苦笑
ちなみに上の問題は本の中にも登場し、難易度は(★4のうち)★2のモノ。
解法を見れば「あぁ」と思う事でしょう。
で、この面積迷路の考え方・解き方にスッキリすると思います。
以下、解法