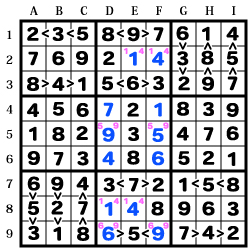
不等号ナンプレ 解き方のコツ
基本ルール
問題は「ナンプレSuper Vol.11」 Q67より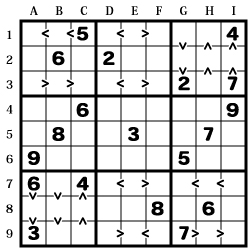
基本は数独(ナンバープレイス)と同じです。
一部、マスの間に不等号があり、
その大小関係から数字を予測します。
始める前に…
やはり最初に確認しておくべきは「不等号」の向き。
問題によっては最初の段階で「1」「9」が固定できるモノもあります。
手順-1
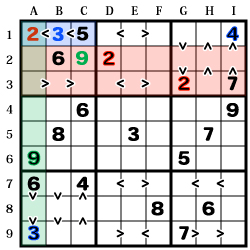
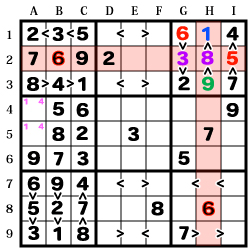
【ABC-1】を見た場合、
【B1】【A1】の順に「5」より小さい数字となっています。
が、【I1】に「4」があり、【A9】に「3」があるので
【B1】に「3」、【A1】には「1・2」が入る事が判ります。
更に【D2】の「2」、【G3】の「2」によって
【A1】は「2」である事が決まります。
※追記:実際には【A1】が「1」、【A2】が「2」の可能性も残ってました^^;
また【A6】の「9」に注目すると、
「9」の入る可能性があるのは【B3】【C2】【C3】となりますが、
不等号を見ると「9」以上の数字は存在しないので、
【B3】【C3】に「9」が入る事は有り得ません。
よって【C2】の「9」が確定します。
手順-2
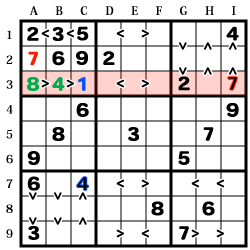
【C3】に注目します。
【ABC-3】では不等号が2つ続き、
その中で一番小さい数字が入る事になります。
この区画で使用していない数字は「1・4・7・8」
【C7】に「4」がある事から
【C3】には「1」以外、入れられない事が判明します。
また【I3】の「7」により、【A2】の「7」が確定。
残ったマスは不等号の向きから、
【A3】が「8」、【B3】が「4」に決まります。
手順-3
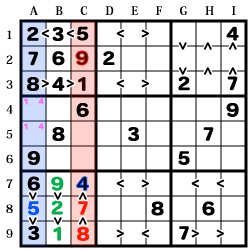
A列を見ると残り3マス、残っている数字は「1・4・5」です。
【A8】に注目すると【C7】に「4」があるので、4は除外。
更に「6より小さく3より大きい」が条件なので「5」と確定します。
【ABC-789】に注目します。
この中で残っている数字は「1・2・7・8・9」
【C8】【C9】は「4より大きい数字」が条件。
条件を満たしている数字は「7・8・9」ですが、
【C2】の「9」から【C8】【C9】は「7」「8」と判ります。
残った「1・2・9」を不等号に合わせて入れれば
この区画は全て埋まります。
手順-4
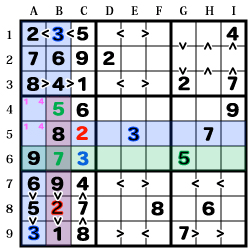
次は【ABC-456】を見ます。
【A9】【B1】【E5】の「3」から【C6】の「3」が、
【B8】の「2」から【C5】の「2」が確定します。
この区画で残っている数字は「1・4・5・7」ですが、
「1・4」は【A4】【A5】で二択状態になっているので候補から排除します。
残る「5・7」が【B4】【B6】に入る事になりますが、
【G6】に「5」がある事から
【B4】は「5」、【B6】は「7」と決まります。
手順-5
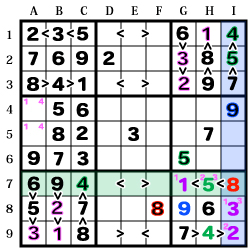
【GHI-123】を見ます。
よく見ると不等号の向きが偏っていて、
一番小さい数字で空いているのは【H1】のみとなっています。
なので、当然ここは「1」が決まります。
【I2】は「7より小さく4より大きい」が条件。
可能性としては「5・6」ですが【B2】の「6」により「5」が確定。
同時に【H8】の「6」により【G1】の「6」も確定します。
ここまで埋まると、不等号の向きから
【H3】には「9」以外の数字が入らない事が判ります。
更に【G2】は「6より小さく2より大きい」数字なので「3」
最後のマスに「8」が入ります。
手順-6
次は【GHI-789】を見ます。
【I4】に「9」がある事から、
不等号と絡むマスに入れない「9」は【G8】と決まります。
【F8】の「8」により、不等号に絡む最大の数字が「8」と判ります。
なので不等号の向きから【I9】の「8」が決まります。
ここからは不等号を気にせず、普通のナンプレの方法で。
【B9】【H1】の「1」から、
「1」の候補は【G7】【I8】の二択。
【B8】【G3】の「2」から、
「2」の候補は【H7】【H9】【I9】と3箇所になりますが、
【I9】に「1」が入る可能性が無い為、
【H9】に「2」が入る可能性も無くなります。
【A9】【G2】の「3」から、
「3」の候補は【H7】【I8】の二択。
【C7】【I1】の「4」から【H9】の「4」が確定。
【G6】【I2】の「5」から【H7】の「5」が確定。
二択候補のマスが埋まってしまったので、
【I8】に「3」、【I9】に「2」、【G7】に「1」が入ります。
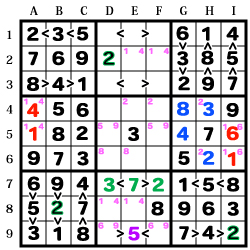
手順-7
【GHI-456】を普通の方法で確認していくと、
「3」「2」「8」「4」が確定。
結果、保留状態だった【A4】【A5】が「4」「1」と確定。
その結果から【I5】【I6】の「6」「1」も確定していきます。
他の区画も二択に絞れる箇所を確認していくと…
【B8】【D2】【I9】の「2」により、候補が【E7】【F7】になります。
が、【F7】に「1」が来る可能性は無いので【F7】が「2」と決まります。
「3」は普通に確定。
7行では残るマスが1つになったので、使っていない「7」を入れます。
【DEF-9】に入る数字は「5・6・9」と判明。
不等号の向きにより、【E9】には一番小さい「5」が確定します。
手順-8
【DEF-789】の一部が確定した事で
【E4】の「2」、【F3】の「3」、【D3】の「5」が決まります。
3行で残るマスが1つになったので、使っていない数字「6」が入ります。
また【C2】の「9」により、【DEF-1】に「9」が入る事が判り、
不等号の向きから【E1】が「9」と確定できます。
【F8】の「8」により【D1】の「8」が、【F1】の「7」が確定。
その流れで【E6】の「8」も確定します。
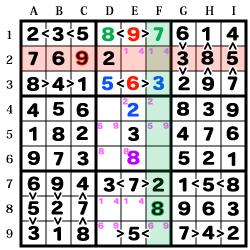
手順-9
【D3】の「5」が確定した事により、
保留状態だった【D5】【F5】の「9」「5」が決定。
更に【D9】【F9】も「6」「9」と決定。
あとは通常のやり方で【F6】の「6」、【D6】の「4」、
二択が崩れて【D8】【E8】の「1」「4」、
【E2】【F2】の「1」「4」、
【D4】の「7」、【F4】の「4」が確定して完成です。
 伊豆・伊東情報館
伊豆・伊東情報館