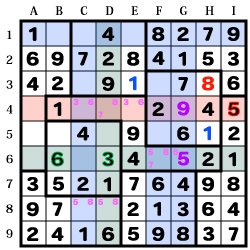
幾何学ナンプレ 解き方のコツ
基本ルール
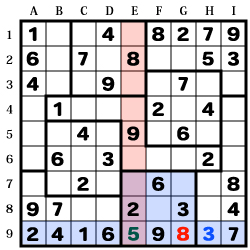
問題は「ナンプレSuper Vol.11」 Q59より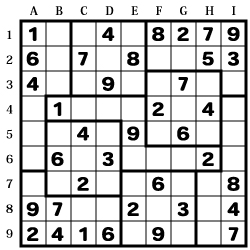
基本は数独(ナンバープレイス)と同じです。
通常、3×3の区画が問題により形状が変化しています。
ナンプレの亜種は比較的難易度が下がっている事が多いのですが、
幾何学ナンプレの場合、形状に惑わされミスが誘発される感じになってます。
始める前に…
基本は表示されている数字が多いモノからでしょうか?
私の場合、面倒なので1〜9の順に調べてますが…
一応、数えてみると
1:3個 2:6個 3:3個 4:6個 5:1個
6:5個 7:5個 8:3個 9:5個
2・4、6・7・9が多いようです。
手順-1
難易度が低くヒントが多いので、いつもと違う視点で。
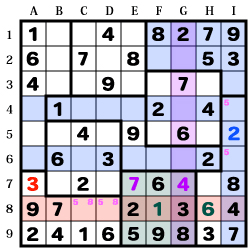
9行を見ると、入っていない数字は「3・5・8」のみ。
そのうち左の区画には既に「3」が存在するので、
【H9】の「3」が確定できます。
残りの2マスを見ると、E列に「8」が存在。
なので【G9】の「8」、【E9】の「5」が確定できます。
手順-2
同様にI列を見ると
右上の区画、4行、6行に「2」が存在する事から【I5】の「2」が確定。
左下の区画では8行の「3」により【A7】の「3」が決まります。
この区画で残っている数字は「5・8」のみとなります。
【C8】【D8】には、必ず「5・8」が入るので、
8行の残っている2マスには「1・6」が入る事になります。
が、下中央の区画には「6」が存在しているので、
【H8】が「6」、【F8】が「1」と判明します。
更にこの区画を見ると、G列に「7」が存在している事から、
【E7】の「7」、【G7】の「4」も確定できます。
手順-3
せっかく数字の数を数えたので…
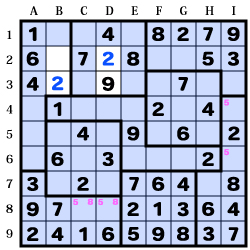
「2」に注目して調べてみます。
「2」が存在する区画・列・行を塗りつぶすと…
上中央の区画で「2」を入れられる場所は【D2】のみ。
当然、左上の区画でも【B3】の「2」が特定できます。
ちなみに…
全て特定できた数字を何かしらの方法で、
確認できるようにしておくと、
無駄な作業やミスを減らせる事ができます。
私の場合、近くに○を3×3で書いて
該当する位置の○を斜線で消しています。
まぁ、後半になると…
一気に進む事が多く、放置状態になりがちですけど。
手順-4
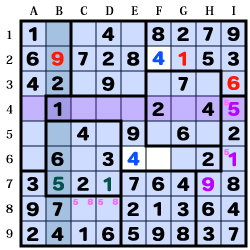
同様に「4」に注目すると【F2】の「4」が確定。
と、同時に【E6】の「4」も確定します。
2行の残り2マスは「1・9」
左上の区画に「1」があるので【G2】に「1」、【B2】に「9」が入ります。
また、右上の区画は残り1マスとなり【I3】の「6」が決定します。
ここまで進めると、初期に確認していたI列が残り2マスに。
チェックしてみると4行に「1」があるので、
【I6】の「1」、【I4】の「5」が確定。
右下の区画が残り1マスとなり【H7】の「9」も確定します。
7行も残り2マスになったので確認してみると、B列に「1」が存在。
これで【D7】の「1」、【B7】の「5」が決まります。
手順-5
数字の「1」に注目すると【E3】【H5】の「1」が決定。
残るH列の1マスは「8」と判ります。
このままだと、ただのナンプレと変わらないので、
幾何学ナンプレならではの見方も。
今回の問題の場合、特徴的なのは中央の区画。
左上、右下もそうだけど、
細長い部分のある区画が攻略の鍵になる事が多いです。
例えば【I4】の「5」に注目すると、
この区画で「5」の入る可能性のある場所は【F6】【G6】の二択になる。
同様に「3・6」に注目すると【C4】【E4】の二択に。と言った感じです。
長い部分に注目する事で候補を減らせる可能性が高くなります。
ここでは普通にG列に注目(苦笑
【G6】は「5」、【G4】は「9」を決めちゃいます。
手順-6
左上の区画に注目すると【A7】の「3」により、【B1】の「3」が。
B列の残り1マス【B5】には「8」が。
F列に注目すると【FGH-345】の区画に「7」が配置済み。
よって【F6】の「7」が確定します。
1行の残り2マスを確認すると【C1】が「5」、【E1】が「6」と判ります。
結果、二択状態になっていた【C4】【E4】が「6」「3」に、
【C8】【D8】も「8」「5」に確定します。
中央の区画では【D4】が残り1マスとなり「8」が確定。
上中央の区画でも【C3】が残り1マスとなり「3」が確定。
F列の二択も【F3】【F5】が「5」「3」に決まります。
ここまで進むと【A4】【A5】【A6】の「7」「5」「8」が確定。
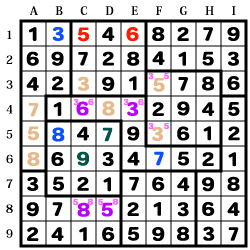
残る【D5】【C6】も「7」「9」と決まって完成です。
 伊豆・伊東情報館
伊豆・伊東情報館