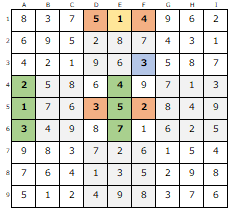
数独(ナンバープレイス) 解き方のコツ
基本ルール
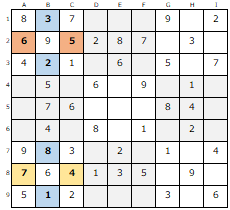
問題は「Standard1500 The数独4」 easy 01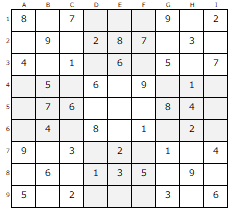
・全ての行・列に1〜9までの数字が重複する事無く入る…A
・各3×3のエリア内に1〜9までの数字が重複する事無く入る…B
始める前に…
1〜9のうち、どの数字が一番多いか、
特定されている数字の多い行・列を確認しておきます。
また、余白に1〜9の数字を書いておくと
処理済の数字が確認できるので便利です。
手順-1
B列を見ると、特定されていない数字は「1・2・3・8」
「1」について考えると【C3】に「1」があるので、
基本ルールBにより【B7】か【B9】となります。
しかし【G7】に「1」があるので、
基本ルールAにより「1」は【B9】にしか入れられないと判ります。
同様に【B3】の「2」、【B1】の「3」、【B7】の「8」が特定できます。
【ABC-123】を見ると、特定されていない数字は「5・6」
A列に「5」、C列に「6」が存在するので
【C2】の「5」、【A2】の「6」が特定できます。
【ABC-789】では、特定されていない数字は「4・7」
A列に「4」、C列に「7」が存在するので
【C8】が「4」、【A8】が「7」と特定できます。
手順-2
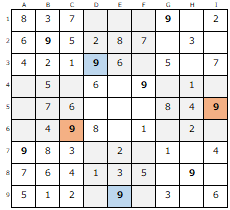
「9」に注目して【DEF-123】を確認すると、【G1】に存在します。
また、【F4】にも存在するので、【D3】の「9」が特定できます。
さらに【DEF-789】では【A7】【F4】、
先ほど特定できた【D3】により【E9】の「9」が特定できます。
同様に【A7】【F4】により【C6】の「9」、
【G1】【F4】【C6】により【I5】の「9」も確定。
全ての「9」が決まった事になります。
余白に書いた数字の9を消し、処理済みとしておきましょう。
手順-3
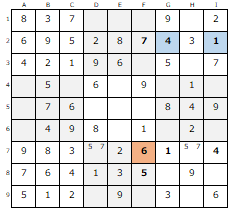
2行を見ると残りの数字が「1・4」です。
【G7】【I7】の「1」「4」から【G2】は「4」、【I2】は「1」と判ります。
7行を見ると、特定されていない数字は「5・6・7」
【F8】に「5」が【F2】に「7」がある為、【F7】の「6」が確定します。
※実際には【F8】に「5」があるので【D7】への「5」の可能性はありませんが…
数字が二択になった場合、
マスの隅に小さく数字をメモしておくと、答えを導く際に役立ちます。
この場合、必ず二択となった場合だけにしましょう。
「とりあえず」な気持ちで、適当にメモをしていくと混乱の元になります。
個人的には、二択の片方が特性した瞬間…
連鎖的に他の部分も特定されていく様が好きです。
手順-4
既に判明している【D7】の「7」、【H7】の「5」を確定。
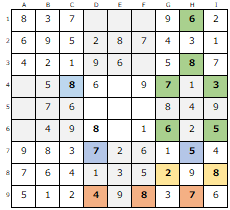
C列では計8個の数字が特定できているので【C4】の「8」を埋めておきます。
9行の残る数字は「4・7・8」
【DEF-789】には「7」があるので【H9】に「7」が。
【D6】の「8」により【F9】の「8」、【D9】の「4」が決まります。
8行では、あと「2・8」
【G5】【I1】を見れば【G8】へは「2」、【I8】へは「8」と判ります。
同様にG列・H列・I列を見ていくと
【G4】【G6】が「7」「6」、
【H1】【H3】が「6」「8」、
【I4】【I6】が「3」「5」が確定します。
手順-5
3行では8個の数字が特定されたので【F3】には「3」を。
D列では【D1】【D5】の「5」「3」
F列では【F1】【F5】の「4」「2」が特定できます。
これにより1行では8個の数字が確定。【E1】へ「1」が入ります。
4行・5行・6行もそれぞれ
【A4】【E4】が「2」「4」、
【A5】【E5】が「1」「5」、
【A6】【E6】が「3」「7」が決まり完成となります。
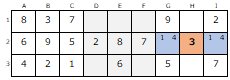
パターン-A
2行を見ると、1〜9のうち
既に特定された数字は「2・5・6・7・8・9」で
特定されていない数字は「1・3・4」となっています。
【G2】【I2】が「1」「4」の二択になった場合、
あふれた「3」が【H2】に入る事が特定できます。
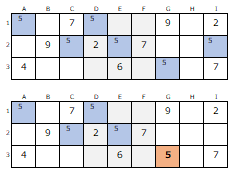
パターン-B
同じ数字が3区画の全てで二択状態になった場合。
【ABC-123】【DEF-123】では1行、2行が、
【GHI-123】では2行、3行で「5」が二択になっています。
しかし【I2】に「5」が入ると
【A1】【D1】が「5」になってしまいます。
よって【I2】に「5」が入る可能性は消え、【G3】の「5」が確定できます。
パターン-C
同じ区画に3つ以上の数字が二択になった場合、
よく見ると確定できる事があります。
【A1】は「5」か「8」
【C2】は「5」か「8」、「1」のようになっている場合…
【C2】に「1」が入ると「5」「8」は行き場を失ってしまいます。
結果【C3】の「1」が確定できます。
パターン-D
意外と見落としがちなパターン。
【G2】【I2】が「1」「4」の二択状態。
【GHI-123】をよく見ると、
特定されている数字は(仮も含めて)「1・2・3・4・5・7・9」
特定されていない数字は「6・8」です。
なので【H1】【H3】は「6」「8」の二択が決まります。
 伊豆・伊東情報館
伊豆・伊東情報館